Nu!
Atunci unde s-a comis gresala?
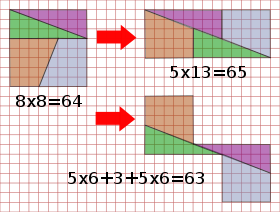
Eroarea trebuie cautata in inexactitatile linilor ce alcatuiesc figurile geometrice obtinute in urma sectionarii tablei de sah. Mai exact in triunghiurile si trapezele ce alcatuiesc dreptunghiul pentru care se calculeaza aria 5×13=65.
La o rezolutie mai mare linile arata asa:
Zona evidentiata in rosu in diagrama de mai sus are forma unui paralelogram foarte lung. Acesta este responsabil pentru diferenta de arii calculate, cea a patratului de 64 si cea a dreptunghiului de 65.
Matematicienii pentru rezolvarea acestui paradox au apelat la sirul Fibonacci (Fn).
Sirul Fibonacci nu este altceva decat o secventa de numere cu proprietatea ca fiecare numar este definit ca suma a doua numere imediat anterioare Fn+1=Fn+Fn-1 pentru toate n = 1, 2, 3, …
Valorile de pornire sunt date de F0 = 0 şi F1 = 1 iar sirul lui Fibonacci va arata asa:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
In acest context Paradoxul tablei de sah pare sa spuna ca
Fn . Fn este egal cu Fn +1 . Fn-1
Daca se fac cateva calcule simple se poate vedea ce se intampla cu adevarat:
Fn. Fn = Fn (Fn-1 + Fn-2) = Fn. Fn-1 + Fn. Fn-2
şi
Fn +1. Fn-1 = (Fn + Fn-1) Fn = Fn-1. Fn-1 + Fn-1. Fn-1
Dn – Diferenta dintre aceste doua produse este:
Dn = Fn +1. Fn-1 – Fn. fn
= Fn-1. Fn-1 – Fn. Fn-2
=-Dn-1 = (-1) 2 = Dn-2 … = (-1) N-1D1 = (-1) n
deoarece D1 = F2. F0 – F1. F1 = 1. 0 – 1. 1 = (-1) 1.
Prin urmare, am stabilit adevarul a ceea ce este cunoscut sub numele de identitate Cassini:
Fn +1. Fn-1-Fn. Fn = (-1) n
Concluzia
Se poate reorganiza intotdeauna un Fn x Fn patrat intr-un 1 x Fn Fn-1 dreptunghi, iar diferenta dintre ariile lor, si anume Fn. Fn respectiv Fn +1. Fn-1, este (-1) n, si anume, fie -1 sau +1.
In primul caz, exista o suprapunere intre figurile geometrice obtinute.
In al doilea caz, exista o ruptura intre ele.
In cazul tablei de sah, exista o ruptura intre cele doua figuri, ruptura identificata cu un paralelogram a carui arie este 1.